Binary To Bcd Verilog

Posted By admin  On 17.08.21

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators. I need help to make the code in VHDL of a converter 6 binary bits to two 7-segment displays. I need to convert binary to BCD first, but I can not do that. Module binarytoBCD (indata, ones, tens, hundreds) input. Binary to Bcd with Verilog.

Binary Coded Decimal format is a binary encoding of decimal numbers that represents each decimal digit by a fixed binary number. For example, 42 is represented in BCD format by the binary representations of 4 and 2, as shown above. The BCD format is common in electronic systems where numeric digits are displayed, as well as in systems where the rounding and conversion errors introduced by binary floating point representation and arithmetic are undesirable.

Each shift effectively doubles the value of the binary number in the four bit shift register which is going to hold the converted BCD digit. Each time a bit is. Bin2bcd.v: Parametric binary to BCD converter using double dabble / shift and add 3 algorithm bcd7seg.v: BCD 7-segment decoder bin2bcdtest.v: Test circuit for the binary to BCD circuit using DE2-115 Development board / Cyclone IV.

We will focus on designing a conversion circuit that converts a BCD formatted number to to a binary formatted number. I chose to detail this direction of conversion as binary to BCD conversion circuits are easily be found by a quick web search.

Binary to bcd verilog code

We will consider two algorithms to perform the conversion, the first being a direct arithmetic approach, and the second an iterative algorithm using a finite state machine with data path (FSMD).

We will be designing for the Basys 2 FPGA board which has 8 input switches. We can use the 8 input switches to encode 2 BCD numbers of 4 bits each. We will therefore concern ourselves with designing a circuit to convert a 2 digit BCD number to a 7 bit binary representation (27 = 128 > 99, the largest 2 digit BCD number we can input).

The first algorithm will simply take the “tens” BCD digit, multiply it by 10, and add the “ones” digit to it. For the conversion of BCD 42, 4 is multiplied by 10, and 2 is added to it, giving us 101010, which is the binary representation of 42.

The inputs are 4-bit bcd1 and bcd0, with the output being the converted 7-bit binary representation, bin. We simply multiply bcd1 by 10, add to it a 7-bit adjusted bcd0, and assign it to the output.

To test the circuit, we can route the binary output to a binary to hexadecimal 7-segment multiplexing circuit, which was detailed in my “Stopwatch with the Basys 2 FPGA” blog.

While not a complete testbench, below are a couple of the tested outputs.

From the input switches we can see that BCD 0100 0010, or 42, gives us 2A in hex, which is decimal 42.

Testing the upper limit, BCD 1001 1001, or 99, gives an output of hex 63, which is decimal 99.

Next we will consider an iterative algorithm that will also convert our 2 BCD digits to a 7-bit binary representation. We will have two 4-bit registers for bcd1 and bcd0, as well as a 7-bit binary answer register, bin.

The algorithm is as follows:

  1. Right shift bcd1, with the LSB shifting to the MSB of bcd0.
  2. Right shift bcd0, with the LSB shifting to the MSB of bin.
  3. If bcd0 is now > 4, subtract 3
  4. repeat steps 1-3, 7 times.

Lets illustrate this with the example of converting BCD 42, 0100 0010, to binary 42, 0101010.

To implement this algorithm we will use a FSM with data path to control the overall operation of the circuit. When in the idle state and a start signal is asserted, the state will change to operate, in which the FSM will iterate through the 7 bits like the algorithm shown above. Once the algorithm completes, the state will change to done, which will assert a done_tick, and then go back to idle.

Lets look at the code implementation in chunks.

We define our symbolic states for the FSM operation to be idle, op for operation, and done. The internal signals are declared for registers and their next state logic, for the state (state), converted binary value (bin), iteration variable (n), and BCD inputs (bcd1 & bcd0).

Above we implement the state and data registers, resetting them when reset is asserted, and assigning their next-state logic values at each positive clock edge.

The FSMD next-state logic determines what happens in each state and how a state transition occurs. Assignments before the case statement are defaults that are only changed if overwritten in the case statements. For example, done_tick is normally 0, unless the FSM is in the done state, in which it is set to 1.

In the idle state, the ready line is asserted, and if the start input is asserted, the next state will transition to op, and n_reg is set to 7, the number of iterations.

In the op state the iterative algorithm is achieved by right shifting in the LSB of bcd0 to bin, right shifting in 0 to bcd1, right shifting in the LSB of bcd1 into bcd0, checking if bcd0 is greater than 4, and if so subtracting 3. This happens 7 times until n_reg = 0, in which the state transitions to done.

In the done state, a done_tick line is asserted, letting a possible dependent system know the operation has completed, then the state transitions back to idle.

The final converted binary value in bin_reg is assigned to the output line, bin.

Since the FSMD iterative algorithm requires a finite time to compute, our test circuit has a master FSM that will idle until the start line is asserted, perform a conversion, receive a done tick, and go back to idling.

Binary

We can see that unlike before where the result was always routed to the output display, we now have to enable the start line to compute the conversion. The intermediate state showing “88” occurs only when the button is pressed and the master FSM rapidly cycles through its states, until it is disengaged. This could be remedied by instead implementing a positive edge detection circuit for the start button input signal.

Computers understand binary number system while humans areused to arithmetic operations in decimal number systems. To enhanceComputer-Human relationship in this perspective, arithmetic operations areperformed by the computer in a binarycoded decimal, (BCD) form.

Binary To Bcd Conversion Verilog Code

In this article I’ll analyse and design a BCD adder whichrequires a minimum of nine inputs and five outputs, four bits are require tocode the aguend and the addend making eight bits, and the circuit input carrymakes the nine inputs. The four bit sum output and the output carry representsthe five outputs.
Binary to bcd conversion verilog code
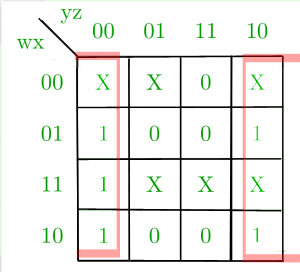
Consider adding 9+9+1 in decimal, the result is 19, instraight binary this should produce an output 100112, this is aninvalid number in BCD, because in BCD code the group of four bit binary onlyrepresent decimal numbers 0-9. The table bellow shows decimal numbers 0-19 withtheir corresponding binary and BCD codes. The K and C in the table are therespective binary carry and BCD carry bits.

Bellow the ruled level on the table, the BCD adder should detectthat the binary codes are unusable in BCD coding system and provide thenecessary correction. The conditions for the levels on the table wherecorrection is required a;
  1. Point where binary sum has output carry K =1 or,
  2. where Z8 and Z2 are both = 1 or,
  3. where Z8 and Z4 are both = 1.
The gives the expression for correction requirement: Cor = K + Z8Z4+Z8Z2
When Cor = 1, it is necessary to add 0110 to the binary sumand provide an output carry for the next stage.



















Figure 1: Block diagram of BCD adder
When an output carry K = 0 nothing happens as the out S8S4S2S1 is added to 0000 in the second4-bit adder, but when K=1 OR Z8&Z4 OR Z8&Z2 is equal to ‘1’, the output carry generates a ‘1’, thus “0110”is added to the output of the first 4-bit adder. The MSB 0 and LSB 0 in the“0110” to be added is generate by the EXOR gate which accept the output carryat its two input, either the output carry is 0 or 1 the EXOR generates a ‘0’(both its input are equal).
The CBCD is the carry generated by the BCD adder,whenever the output of the OR-gate is ‘1’ a carry is generated by the BCD adderto the next four-bit group of the BCD code, carry output generated by the 4-bit adder of the second stage is discarded as it will provided by CBCD as required. Bellow is the Verilog HDL code forBCD adder and figure 2,3, and four shows the simulations changing the bitsvalue at 100ns, 200ns and 300ns.
//-----------------------------------------------------
input [3:0] A, B;

output C;
wire C1, C2, C3, C4,C5;
and (C1, Z[3], Z[2]);
or (C, C3, C1,C2);

Binary to bcd verilog
assign X[1] = C;
assign X[0] = C5;

four_bit_adder F_1 (Z,C3, A, B, C0);

//----------------------------------------------------------

//-------------------------------------------------------------
// Test bench forBCD_Adder
wire [3:0] S;
reg [3:0]A, B;
Binary To Bcd Verilog


begin
#100 A[3:0] = 4'b1000;B = 4'b0011; C0 = 1'b0;

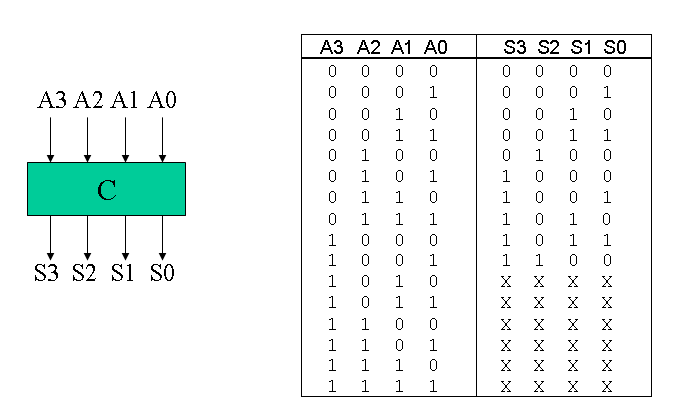
Convert Binary To Bcd Verilog

initial #400 $finish;
//--------------------------------------------











Figure 2:Simulation showing the initial bits value of A: 0000, B: 0000, Sum S: 0000 andCarry C: 0 for the BCD adder (i.e. 0 + 0 = 0 0).












Figure 3:Simulation showing the bits value at 100ns for A: 1001, B: 1001, Sum S: 1000 and Carry C: 1 for the BCD adder (i.e. 9 +9 = 1 8 ).











Figure 4:Simulation showing the bits value at 300ns for A: 1000, B: 0011, Sum S: 0001 and Carry C: 1 for the BCD adder (i.e. 8+3 = 1 1 ).

16 Bit Binary To Bcd Verilog Code


Figure 5:Simulation showing the bits value at 300ns for A: 0100, B: 0011, Sum S: 0111 and Carry C: 0 for the BCD adder (i.e. 4+3 = 0 7 ).
Reference
Mano M. Morris andCiletti D. Michael; “Digital Design With and Introduction to the VerilogHDL – Fifth Edition” Copyright © 2013, 2007, 2002, 1991, 1984 Person Education,Inc., publishing as Prentice Hall, One Lake Street, Upper Saddle River, NewJersey 07458.